Pyramid connections

Pyramid connections

It has been suggested that the Egyptians liked connecting their buildings, monuments, and pyramids by angles, ratios, and maximum tilt, but are there any more links?

Pyramids 
From measurements of Khufu's pyramid and using the ratio:

half base perimeter ÷ height = π

(½ base ÷ h = π)(0.004 off and in meters)

It can be shown that if this ratio means anything, then it can be shown that the actual height of Khufu's pyramid was only 139 m and never 146.7 m.

(whole perimeter = error × 2)

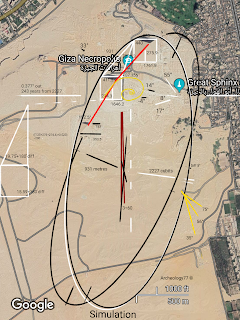
The ratio error equals 0.1778, and when converted into km/° is equal to 19.765 km. This distance has already been shown to be the Red Pyramid's distance (235 m short if not measured from the center).

The pyramids have angles of 20°, 21°, and 23° (with Giza), with the angles from the Bent Pyramid at 19°, 20°, and 21° (with Giza, and at a distance of 22 km).

(This error number in metres is also the width of Khufu's lower south shaft at 0.1778 metres.)

It has already been shown that the ancient builders linked pyramids, thus increasing the significance of the old with the new.

For example, the Sphinx is 243 years off from an east/west 0° tilt line at maximum tilt 1985.

This maintains the importance, and the link is the error ratio derived from a ratio divided by 2 off aligning the constellation of Orion (the error is 24.3m).

They have then carried this through to the alignment of the pyramids and further builds that align with the areas Baalbek and Jerusalem (possibly no longer existing, although they might have built the base at both locations).

Menkaure

Menkaure's pyramid also links in several ways (making it offset from Orion):

(1) with the total heights × royal cubit - 200 (((125 + 276 + 274) × 0.523) - 200) (this number also gives the separation distance, hence 24.3 metres) and

(2) the angle produced by rotating the constellation 180° is 15.59° + 180° and 19.75° + 180°, thus producing two different widths at 192.5° of 199 and 195 cubits.

(Some have considered this a construction anomaly) 

(Thus, the use of π and its error rather than coincidentally just very near was that they were building pyramids, and if an error occurred, they would offset it into the construction of another (but one angle of connection wouldn't be enough).

Another ratio link that occurs in Khufu's pyramid is the height divided by half the base width in metres.

(h ÷ ½ base width = φ)

This equals the square root of the golden ratio.

A ratio that already links the slopes to Khafre's pyramid and a π circle to a φ circle.

146.7 ÷ 115.2 = √φ with an error of 0.00143 with the height of 146.6 metres equaling zero.

(146.6 = 280.31 cubits)

(When using a more accurate base measurement, the following height is produced:

√φ × 115.15 = 146.472 which equals 280.06 cubits in height.)

The heights between 139 m and 146.6 m are equal to Khufu's pyramid shaft width, with the height of 146.472 m equal to zero in a triangular ratio.

For the base × √φ to equal the height, the slope would need to be 0.04° less.

51.827−51.867=0.04°

This would affect the connections between the slopes and, at the slope length, would be 13 cm less.

This is not the only pyramid that lacks a peak, so there could be two different answers, with the possibility of Khufu's being constructed without a peak.

Khafre

Another ratio is half perimeter divided by height.

(½ perimeter ÷ h)

(The use of π in these suggests a semicircle, and 2π suggests a 360° circle, but the errors double in size. Different heights are included.)

Khafre
Perimeter 1646.2715 (860.99m)
Height 274.3785
Ratio 6.0

143.5m
(1646.2715÷2)÷274.3785=3.0-π=0.1415917424 (in cubits/m)
136.4m
((1646.2715×0.523)÷2)÷(136.4)=3.1561583376−π=0.01456568

Khufu
Perimeter (230.253+230.454 +230.391+230.357)=921.455m
Cubits 1761.864 (1761.864÷2)÷(275.9655) =3.192−π=0.05
Ratio 6.384

265×0.523=138.6
(921.455÷2)÷138.6=3.324

3.324−π=0.1827

275.9655×0.523=144.33m
(921.455÷2)÷144.33
3.1922−π=0.0506

280×0.523=146.4m

(921.455÷2)÷146.4=3.1462

3.1462−π=0.00459

Although the difference between the measured and expected values is 0.04565.

0.0506 - 0.00495 = 0.04565

The measured height of 275 is near to the separation angle in Khufu's pyramid (being halfway between 0.05 and 0.052).

Khafre's pyramid is 260 cubits (136.4 m), which is very near to 1 - 1.0145°.

Considering that all pyramids are already linked together by the star separation of Orion and the error in rotation both ways, Khafre's pyramid does not need to link any further.

Khufu
Khufu's slope is linked with the error of Menkaure's pyramid positioning. Menkaure's slope is linked to the cubit. Khafre's slope is linked to the root of the golden ratio and separation angle. π linking to φ through a volumetric shape with ratio √φ, this also links to Khafre's slope.


Ratios
This ratio, linked with π but through the measured height of 275 cubits in Khufu's pyramid, demonstrates that if it is connected with π, it is more likely that the measured height of 275 cubits is the correct measurement, along with the shorter one of 265.4 cubits.

With Khafre's pyramid, the ratio of the heights shows that the taller one, measured along with the shorter Khufu's, is the correct height, giving the important separation distance.

Menkaure's pyramid's position relies on this separation distance. (((125+276+274.4)×0.523)-200)=153.2 cubits

As opposed to (((125+276+265.4)×0.523)−200)=148.5 cubits

Menkaure's pyramid 195/200 cubits half base ÷ height
(195÷2)÷125=0.78
(200÷2)÷125=0.8

The difference produces 0.02 half perimeter ÷ height
(390)÷125=3.12
(395)÷125=3.16

Using the two numbers, both tall and short, in Khufu's pyramid gives a 0.1827 error ratio.

This is very nearly equal to the lower south shaft width (the difference being 0.005 or 5 mm). The 274.4 cubits produce numbers that don't connect, but this, along with 275.9655 cubits for Khufu's pyramid, must be used or considered.

These different heights should then be used as heights for Khufu's, with the last 7.6 metres not built.

(The varying height could include this small but important variation)

The 4.5-metre difference in measurement could be explained as a possible altar or platform. It has been suggested that whichever appearance is correct for one must be for the other.

Menkaure's pyramid numbers do not seem to link to π until you add them together and divide by 2.

(π=180° and 2π equals 360°)

This does not suggest these are the only interpretations, but most likely the ones they would have chosen as opposed to guessing.

Bent Pyramid 
The connection with the Bent Pyramid, with its slopes and differences.
43.36667-54.46222=11.095
43.36667÷11.095=3.9
54.46222÷11.095=4.9

The difference divided by the slopes produces a difference of 1, usually a ratio, but using a ratio equation with these slopes. (1+√(43.36667)÷(1−√(54.46222))=0.0322 0.0322÷1.55=0.0207796
1000×0.0207796=20.78

One possible interpretation is a distance of 20 kilometers away and 0.78, a ratio of Menkaure's pyramid.

The Bent Pyramid was built just before Khufu's by Sneferu.

Conclusion 

Symbolically, the use of π suggests "never-ending," and π in construction ratios connects with a π circle's link to a φ circle by √φ. The use of π in measurements of the pyramids suggests an error ratio that gives the correct measurements.

The use of π and its error rather than coincidentally just very near was that the ancient Egyptians were building pyramids, and if an error occurred, they would offset it into the construction of another (but one angle of connection would not be enough).

This seems to correlate until too many offsets occur, so further builds are required.

This seems to connect to Baalbek and Jerusalem.

The use of π, √φ, and φ along with the construction ratio of 11/7 follows through these builds. This can be shown to have been included from Khufu's pyramid, the first of the three pyramids built at Giza.

Pyramids
Great Pyramid of Giza 

Archeology77 ©