Down Tor Stone Circle Down Tor Stone Circle is a stone circle near Down Tor, Dartmoor. Also called Hingston Hill Cairn. Foggintor Quarry is not far to the northwest, where the stones could have been quarried, along with Down Tor, which is currently a national park. Crazywell Cross is to the north and Drizzlecombe to the south. Coordinates 50.506060,-3.994103 Description Down Tor Stone Circle consists of a long stone row with a circle of stones at the end towards the southwest. This can be considered similar to Drizzlecombe in shape and construction, and is 2 kilometers away. Measurements This tor and circle are angled at 22° towards the southwest, with the row at a length of 755 feet or 230 metres. Analysis It is possible that Down Tor Stone Circle is similar to Drizzlecombe, which was shown to be possibly connected with the golden ratio and π or 9πφ together. The circle is 40 meters wide. If using the 22° on the circle towards the northwest, then all stones pair...
Pyramid - Construction Ratios
Conclusion
Using exact measurements for Khafre's pyramid for slope and construction with measurements in cubits, then using an overall ratio of 7 by 5.5, gives an angle of 51.843°.
With the construction of the Giza Pyramids, were there anything more to it than just a build ratio of 5.5×7 giving different slopes of between 51°/53°?
It has been shown that the connection for π and golden ratio in a circle is volumetric with a ratio of √φ or π/φ in a 45° angle.
It has been shown that the connection for π and golden ratio in a circle is volumetric with a ratio of √φ or π/φ in a 45° angle.
The connection to π and φ in a standing wave (this is included as it connected to pi÷5=36° inside a circle).
2×cos(π÷5)=φ
φ=√((5+√5)÷(5-√5))
Standard Measurements
2 cubits as a length are equal to 1.046m, a standard unit of measure (φ÷√2) has a ratio of 16.5:1 with the φ.
2×cos(π÷5)=φ
φ=√((5+√5)÷(5-√5))
Standard Measurements
2 cubits as a length are equal to 1.046m, a standard unit of measure (φ÷√2) has a ratio of 16.5:1 with the φ.
1.046−1.144=0.098
1.618÷0.098=16.5
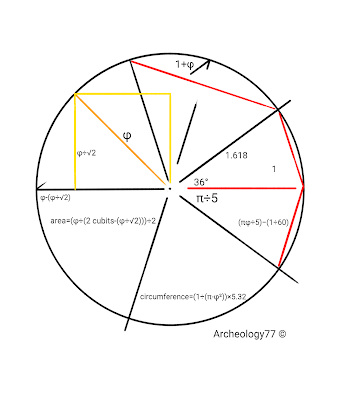
The φ ratio, π and cubit connections for a φ circle of radius 1.618.
Area= (φ÷(2 cubits-(φ÷√2)))÷2=8.22
Area of two circles plus separation distance
2((φ÷(2 cubits-(φ÷√2)))÷2)+(3÷60)=16.5
1.618÷0.098=16.5
The φ ratio, π and cubit connections for a φ circle of radius 1.618.
Area= (φ÷(2 cubits-(φ÷√2)))÷2=8.22
Area of two circles plus separation distance
2((φ÷(2 cubits-(φ÷√2)))÷2)+(3÷60)=16.5
A ⅓ of a 108° shape has a value of one.
(πφ÷5)−(1÷60)=1
(πφ÷5)−(1÷60)=1
Circumference of a circle is 2πr but including the φ is,
Circumference= 1÷(π-φ²)×5.32
Pyramids
In a triangle (a pyramid) with sides 1.618 and slope 51.34° (Menkaure's pyramid), the area is approximately √φ and perimeter 10 cubits. If this was 1.618m, then the error off would be 1.91 cms, and the base would be 2m.
Increasing the slope in factors of ×10 would increase the area by 10².
*At slope=φ the area=√φ and the base=2*
In a triangle with a 51.867° slope (Khufu's pyramid), the ratio gives a difference of 3182 or 100 × 31.82 number.
The slope of 1.618 is much nearer to an area of √1.618 and perimeter of 10 cubits.
The √1.618×½base is equal to the height.
√(1.618)×115.15=146.47m
Also, the best angle to keep a φ is 51.827°, 0.04° less than it has been measured at, at the slope length it is a difference of 13 cms.
(Various heights are considered in other articles. Here it suggests it is equal to √φ×½×base)
A cubit to a pyramid ratio, this is Khufu's pyramid,
(16÷5−0.523)+(16÷5+0.523)=6.4
Circumference= 1÷(π-φ²)×5.32
Pyramids
In a triangle (a pyramid) with sides 1.618 and slope 51.34° (Menkaure's pyramid), the area is approximately √φ and perimeter 10 cubits. If this was 1.618m, then the error off would be 1.91 cms, and the base would be 2m.
Increasing the slope in factors of ×10 would increase the area by 10².
*At slope=φ the area=√φ and the base=2*
In a triangle with a 51.867° slope (Khufu's pyramid), the ratio gives a difference of 3182 or 100 × 31.82 number.
The slope of 1.618 is much nearer to an area of √1.618 and perimeter of 10 cubits.
The √1.618×½base is equal to the height.
√(1.618)×115.15=146.47m
Also, the best angle to keep a φ is 51.827°, 0.04° less than it has been measured at, at the slope length it is a difference of 13 cms.
(Various heights are considered in other articles. Here it suggests it is equal to √φ×½×base)
A cubit to a pyramid ratio, this is Khufu's pyramid,
(16÷5−0.523)+(16÷5+0.523)=6.4
With
16÷5=3.2
3.2+3.2=6.4
From Nabta Playa, the numbers as sums produce two numbers, 9.128 and 2.68. These applied in the same ratio equals 1.43. (9.128+√(2.68))÷(9.128−√(2.68))=1.43
These then connect in the ratio.
The value of (31.82÷100)×π=1 this equates to the % size of the pyramid shafts to the constellation of Orion. (√((5+√5)÷(5−√5)))÷(π×0.36)=1.43
(√((5+√5)÷(5−√5)))×(31.82)=0.05
In construction, these numbers would have been applied in the following ways. Applying these factors to pyramids, the lower blocks on Khufu's pyramid are 1×1×2.5 in metres, the CoG=1.43634m with a Perimeter of= 3.28284.
For a 1×1 block in metres, if the 2.3 metric ton blocks (1000kg) would actually be 99 cms and 5.6 cms off from 2 cubits, then the measurements used for density and equation would be,
2.323 sandstone
2.692 granite
Volume=mass÷density
The construction process was not limited to stones being of the same dimensions.
16÷5=3.2
3.2+3.2=6.4
From Nabta Playa, the numbers as sums produce two numbers, 9.128 and 2.68. These applied in the same ratio equals 1.43. (9.128+√(2.68))÷(9.128−√(2.68))=1.43
These then connect in the ratio.
The value of (31.82÷100)×π=1 this equates to the % size of the pyramid shafts to the constellation of Orion. (√((5+√5)÷(5−√5)))÷(π×0.36)=1.43
(√((5+√5)÷(5−√5)))×(31.82)=0.05
In construction, these numbers would have been applied in the following ways. Applying these factors to pyramids, the lower blocks on Khufu's pyramid are 1×1×2.5 in metres, the CoG=1.43634m with a Perimeter of= 3.28284.
For a 1×1 block in metres, if the 2.3 metric ton blocks (1000kg) would actually be 99 cms and 5.6 cms off from 2 cubits, then the measurements used for density and equation would be,
2.323 sandstone
2.692 granite
Volume=mass÷density
The construction process was not limited to stones being of the same dimensions.
In building two different ways were used, (1) a foreman would use a predetermined measure length for choosing stones that arrived from quarries, (2) the height of stones were predetermined at quarries and measured in ratios. The casing stones and sandstones for the outside would adhere to smaller tolerances. The slopes would later be carved to an angle of 51-53° with similar coloured mortar being used in binding.
There are various measurements for the casing stones, but using the numbers (link below) 685mm x depth 860mm x height 546mm x length of sloping side 612mm.
For these stones with a slope of 612mm, can be considered as a block and triangle.
There are various measurements for the casing stones, but using the numbers (link below) 685mm x depth 860mm x height 546mm x length of sloping side 612mm.
For these stones with a slope of 612mm, can be considered as a block and triangle.
The block is 0.476m×0.476m and a triangle of 0.476m×0.385m×0.612m.
This gives a side area of 1.14m against a slope of 51°, although with a height of 0.546m, the slope increases to 54°.
Width/height 685×546
Depth 860
Slope 612
Area (0.685×0.546)×0.532×10=1.99
Depth 0.861×0.532=1.618
Slope 0.612×0.532×10=3.2
Khufu's pyramid casing stones are said to be in ratios of 1×1.33×2.66 instead of 1×1×2.
This gives a side area of 1.14m against a slope of 51°, although with a height of 0.546m, the slope increases to 54°.
Width/height 685×546
Depth 860
Slope 612
Area (0.685×0.546)×0.532×10=1.99
Depth 0.861×0.532=1.618
Slope 0.612×0.532×10=3.2
Khufu's pyramid casing stones are said to be in ratios of 1×1.33×2.66 instead of 1×1×2.
The volume multipled by density gives weight, but divided gives one plus a cubit.
3.5378×2.323=8.22 tons
3.5378÷2.323=1.523
3.5378÷2.323=1.523
Construction Ratios (π ÷ 2)
Another possibility for a construction ratio of 11 by 7 is that these numbers divided equal half π.
π ÷ 2 = 1.5707963268
11 ÷ 7 = 1.5714285714
1.5714285714 - 1.5707963268 = 0.0006322462
For the construction ratios to equal (π÷2), a more accurate ratio is chosen, and then a number accurate to ten decimal places.
11 ÷ 7.002799 = 1.5708004756
11 ÷ 7.0028175031 = (π ÷ 2)
As a ratio, if in metres as 11 metres by 7 metres, this would be about 3 millimeter difference.
Conclusion
Using exact measurements for Khafre's pyramid for slope and construction with measurements in cubits, then using an overall ratio of 7 by 5.5, gives an angle of 51.843°.
This shows that although proportions internally were 7 by 5.5 with the slope of the steps, the casing stones could vary slightly, and the difference of the final angle is very near to √φ.
Slope= 342.97322
Height= 274.3786
Base= 205.7839
Inclination=53.13°
Considering that these are the current day measurements with only a few casing stones left, the different proportions of 10.46/7 (5.23/7) could have been a possibility in construction.
Slope= 342.97322
Height= 274.3786
Base= 205.7839
Inclination=53.13°
Considering that these are the current day measurements with only a few casing stones left, the different proportions of 10.46/7 (5.23/7) could have been a possibility in construction.
Comments
Post a Comment